Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Матрицы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Когда речь идет о матрице линейного оператора A = (aik), всегда подразумевается, что в "двух экземплярах" пространства N выбирается один и тот же базис. Матрица линейного оператора квадратна. Матрица тождественного оператора единична. Согласно п. 4, множество 4. Сложение матриц и умножение на скаляр. Пусть A = (aik), B = (bik) - две матрицы одинакового размера над полем A + B = (cik), где cik = aik + bik, aA = (aaik). Эти операции определяют на матрицах данного размера структуру линейного пространства. Легко проверить, что если A = Af, B = Ag (в одинаковых базисах), то Af + Ag = Af + g, Aaf = aAf, так что указанное соответствие (а оно биективно) является изоморфизмом. В частности, dim Композиция линейных отображений описывается в терминах умножения матриц -1-2-3-4-5-6-7-8-9-10-11-12-13-14-15- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
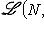
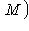 является в свою очередь линейным пространством
является в свою очередь линейным пространством 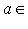
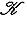 . Положим
. Положим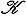
 (размер
(размер 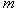
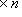 ).
).