Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Матрицы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8. Определитель и след линейного оператора. Положим Tr f = Tr Af = (след - "trace" - матрицы A есть сумма элементов ее главной диагонали); det f = det Af. Инвариантность определителя относительно сопряжения очевидна:
Чтобы установить инвариантность следа, докажем более общий факт: если А, B - такие матрицы, что АВ и ВА определены, то Tr AB = Tr BA. Действительно, Tr AB = Если теперь B невырождена, то, применяя доказанный факт к матрицам B -1A и B, получим Tr(B -1AB) = Tr(BB -1A) = Tr A. В заключение приведем определения, названия и стандартные обозначения для нескольких классов матриц над вещественными и комплексными числами, исключительно важных в теории групп и алгебр Ли и ее многочисленных приложениях, в частности в физике. Первый класс образуют так называемые классические группы: они действительно являются группами относительно матричного умножения. Второй класс образуют алгебры Ли: они составляют линейные пространства и устойчивы относительно операции взятия коммутатора: [A, B] = AB - BA. -1-2-3-4-5-6-7-8-9-10-11-12-13-14-15- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
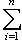
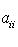 , где Af = (aik)
, где Af = (aik)
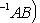
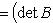
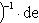
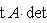
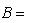
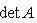
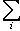
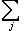
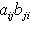 , Tr AB =
, Tr AB = 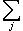
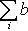
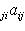 .
.