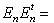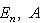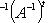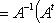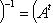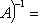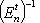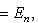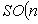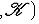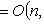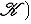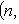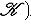Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Развесные табаки для самокруток еще в Украине
|
Линейные пространства и линейные отображения / Матрицы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
9. Классические группы. а) Полная линейная группа GL(n, б) Специальная линейная группа SL(n, В этих двух случаях в) Ортогональная группа O(n,
наконец, (AB)(AB)t = ABBtAt = AAt = En. При г) Специальная ортогональная группа SO(n,
Вместо SO(n, R) обычно пишут SO(n). -1-2-3-4-5-6-7-8-9-10-11-12-13-14-15- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

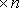 над полем
над полем