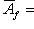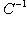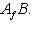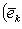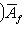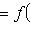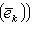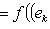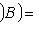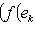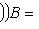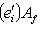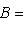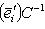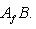Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Матрицы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Матрица A называется матрицей перехода (от нештрихованного базиса к штрихованному), или от штрихованных координат к нештрихованным. Заметим, что она обратима: обратная матрица есть матрица перехода от штрихованного базиса к нештрихованному. Заметим, что формулу В физике эти две точки зрения называются соответственно "пассивной" и "активной". В первом случае мы описываем одно и то же состояние системы (вектор l) с точки зрения разных наблюдений (со своими системами координат). Во втором случае наблюдатель один, а состояние системы подвергается преобразованиям, состоящим, например, из симметрий пространства состояний этой системы. в) Матрица линейного отображения в измененных базисах. В ситуации п. 3 выясним, как изменится матрица Af линейного отображения, если перейти от базисов {ek},
В самом деле, вычисляя в базисах, имеем
-1-2-3-4-5-6-7-8-9-10-11-12-13-14-15- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

 можно было прочесть также как формулу, выражающую координаты старого вектора-столбца
можно было прочесть также как формулу, выражающую координаты старого вектора-столбца 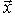 через координаты вектора
через координаты вектора 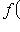
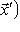 , где f - линейное отображение
, где f - линейное отображение 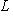
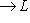 , описанное матрицей A в базисе {ek}.
, описанное матрицей A в базисе {ek}.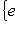
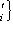 к новым базисам
к новым базисам 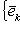
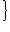 ,
, 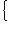
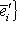 пространств N, M. Пусть B - матрица перехода от {ek}-координат к
пространств N, M. Пусть B - матрица перехода от {ek}-координат к 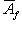 отображения f в базисах
отображения f в базисах