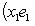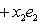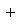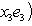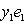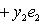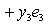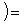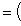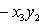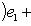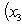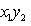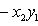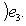Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Трехмерное евклидово пространство / 1 2 3 4 5 6 7 8 9 10 11 12 13
Пусть
Это завершает доказательство. Операторы 9. Векторное произведение. Пусть {e1, e2, e3} - ортонормированный базис в
Замена базиса на другой, ориентированный так же, не меняет векторное произведение; если же новый базис ориентирован противоположно, то у него меняется знак. -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
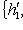
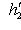
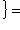
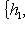
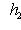
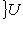 . Поскольку оба базиса ортонормированы, матрица перехода U должна быть унитарна. По следствию
. Поскольку оба базиса ортонормированы, матрица перехода U должна быть унитарна. По следствию 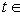
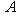 матрица tA эрмитова, а оператор exp(itA) унитарен, и можем положить
матрица tA эрмитова, а оператор exp(itA) унитарен, и можем положить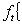
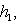
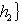
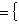
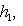
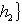
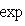
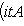
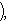
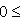
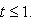
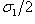
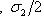
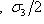 в
в 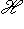 называются наблюдаемыми проекцией спина на соответствующие оси в
называются наблюдаемыми проекцией спина на соответствующие оси в 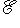 : эту терминологию объясняет квантовомеханическая интерпретация из п. 5. Множитель 1/2 введен для того, чтобы их собственные значения были равны
: эту терминологию объясняет квантовомеханическая интерпретация из п. 5. Множитель 1/2 введен для того, чтобы их собственные значения были равны 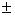
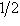 .
.