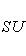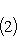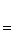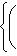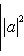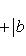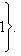Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Трехмерное евклидово пространство / 1 2 3 4 5 6 7 8 9 10 11 12 13
Ядро гомоморфизма Смысл построенного гомоморфизма выясняется в топологии: группа SU(2) односвязна, т. е. любую замкнутую кривую на ней можно непрерывным движением стянуть в точку, тогда как для SO(3) это неверно. Таким образом, SU(2) является универсальным накрытием группы SO(3). Воспользуемся доказанной теоремой для того, чтобы разобраться в структуре группы SO(3), играя на том, что SU(2) устроена проще. Здесь уместно процитировать Р. Фейнмана: "Не правда ли, странно, что, живя в трех измерениях, мы все же с трудом воспринимаем, что произойдет, если сперва повернуться так, а потом еще как-нибудь. Вероятно, если бы мы были птицами или рыбами и если бы мы на собственном опыте знали, что бывает, когда все время крутишь разные сальто в пространстве, нам было бы легче воспринимать подобные вещи". 13. Структура SU(2). Прежде всего, элементы SU(2) суть
Множество пар {(a, b) | |a|2 + |b|2 = 1} в C2 превращается в сферу единичного радиуса в овеществлении C2, т. е. R4: (Re a)2 + (Im a)2 + (Re b)2 + (Im b)2 = 1. -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
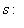
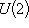
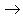
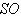
 состоит только из скалярных операторов
состоит только из скалярных операторов 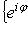
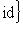 : это следует из предложения п. 7, согласно которому базис
: это следует из предложения п. 7, согласно которому базис 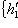
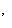
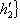 восстанавливается по
восстанавливается по 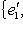
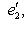
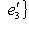 как раз с точностью до умножения
как раз с точностью до умножения 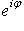 . Пересечение группы
. Пересечение группы 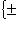
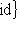 , что и завершает доказательство.
, что и завершает доказательство.
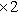 -матрицы с комплексными элементами, для которых
-матрицы с комплексными элементами, для которых 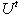
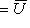 и det U = 1. Отсюда сразу же следует, что
и det U = 1. Отсюда сразу же следует, что