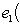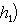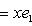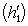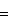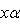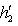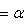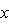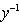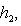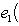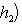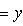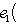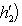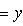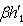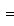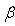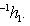Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Трехмерное евклидово пространство / 1 2 3 4 5 6 7 8 9 10 11 12 13
Теперь можем объяснить математический смысл матриц Паули, доказав обратное утверждение. 7. Предложение. Для каждого ортонормированного базиса {e1, e2, e3} пространства
где Ae - матрица оператора e в базисе {h1, h2}. Он определен с точностью до умножения на комплексное число, по модулю равное единице. Доказательство. Собственные значения ei суть Далее,
так что
-1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
 существует ортонормированный базис {h1, h2} пространства
существует ортонормированный базис {h1, h2} пространства 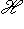 , обладающий тем свойством, что
, обладающий тем свойством, что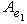
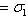
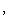
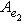
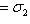 или
или 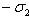
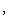
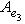
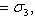 ,
,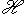
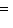
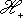
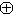
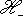 , где e3 действует на
, где e3 действует на 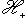 тождественно, а на
тождественно, а на 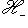 - изменением знака. Выберем сначала векторы
- изменением знака. Выберем сначала векторы 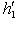
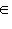
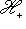
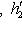
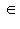
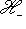
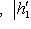
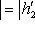
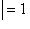 . Они определены с точностью до умножения на
. Они определены с точностью до умножения на 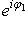
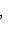
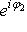 ; матрица e3 в базисе
; матрица e3 в базисе 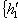
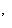
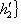 есть
есть 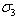 .
.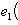
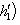
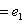
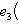
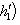
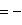
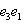
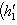
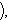
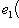
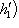 есть нулевой собственный вектор для e3 с собственным значением -1. Поэтому
есть нулевой собственный вектор для e3 с собственным значением -1. Поэтому 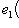
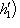
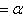
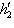 . Аналогично
. Аналогично 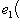
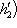
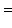
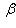
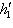 . Матрица e1 в базисе
. Матрица e1 в базисе 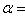
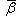 . Наконец,
. Наконец, 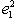
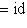 , поэтому
, поэтому 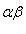
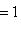
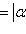
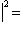
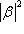 . Заменив
. Заменив 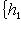
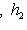
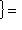
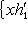
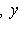
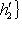 , где | x | = | y | = 1, чтобы превратить матрицу e1 в новом базисе в
, где | x | = | y | = 1, чтобы превратить матрицу e1 в новом базисе в 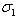 , получим
, получим