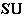
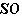
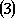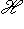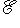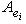
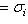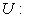
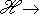
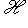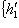
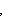
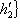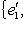
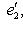
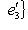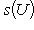
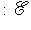
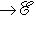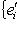
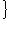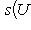
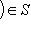
11. Гомоморфизм . Фиксируем ортонормированный базис {h₁, h₂} в и соответствующий ему ортонормированный базис {e₁, e₂, e₃} в , для которого . Любой унитарный оператор переводит {h₁, h₂} в , этому последнему базису отвечает базис , и имеется ортогональный оператор , который переводит {e_i} в . По следствию п. 8 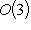, т. к. определитель s(U) положителен.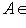

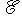Реализовав матрицами в базисе {h₁, h₂}, можем представить действие s(U) на простой формулой:

s(U)(A) = UAU ^-1

для любых . Действительно, это частный случай общей формулы замены матрицы оператора при замене базиса. Можем теперь доказать следующий важный результат.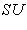

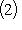
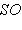
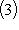12. Теорема. Отображение s, ограниченное на SU(2), определяет сюръективный гомоморфизм групп с ядром .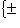

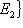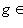
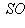
Доказательство. Из формулы s(U)(A) = UAU ^-1 сразу видно, что s(E) = id и s(UV) = s(U)s(V), так что s является гомоморфизмом групп. Его сюрьективность проверяется так.

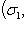
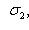
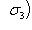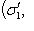
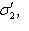
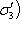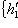
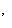
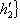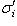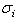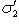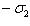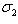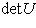
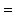
Выберем элемент и пусть g переводит базис в в новый базис . Построим по нему базис в , в котором операторы задаются матрицами . По предложению п. 7 существует с точностью до того, что матрица , возможно, равна , а не . На самом деле эта возможность исключена по следствию п. 8, т. к. 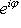сохраняет ориентацию . Оператор U, переводящий {h₁, h₂} в , удовлетворяет условию s(U) = g. Правда, он может принадлежать лишь U(2), а не SU(2). Если , то 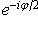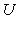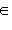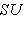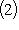. 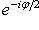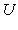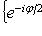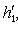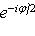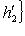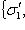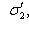Матрица переводит {h₁, h₂} в , а этому базису в 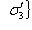по-прежнему отвечает базис в . 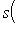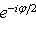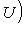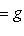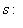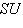Следовательно, также , и получаем, что 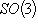сюрьективен.

-1-2-3-4-5-6-7-8-9-10-11-12-13-