Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
6. Следствие. Любая вещественная симметричная или комплексная эрмитова матрица имеет вещественный спектр и диагонализируема. Доказательство. Построим по матрице A самосопряженный оператор в координатном пространстве Rn или Сn с канонической евклидовой или унитарной метрикой и применим теорему п. 5. Из нее видно даже больше: матрицу X такую, что X -1AX диагональна, можно найти в O(n) или в U(n) соответственно. 7. Следствие. Отображение Доказательство. Алгебра Ли u(n) состоит из антиэрмитовых матриц, а любая антиэрмитова матрица имеет вид iA, где A - эрмитова матрица. Чтобы решить относительно A уравнение exp(iA) = U, где 8. Следствие. а) Пусть g1, g2 - две ортогональные или эрмитовы формы в конечномерном пространстве L, и одна из них, скажем g1, положительно определена. Тогда в пространстве L существует базис, матрица Грама которого относительно g1 единична, а относительно g2 диагональна и вещественна. б) Пусть g1, g2 - две вещественные симметричные или комплексные эрмитово симметричные формы относительно переменных x1, ..., xn; y1, ..., yn, и g1 положительно определена. -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
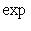
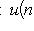
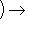
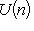 сюръективно.
сюръективно.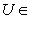
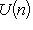 , реализуем U как унитарный оператор f в эрмитовом координатном пространстве Cn. После этого по теореме
, реализуем U как унитарный оператор f в эрмитовом координатном пространстве Cn. После этого по теореме 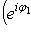

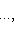
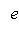
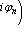 , зададим в этом базисе оператор g матрицей diag
, зададим в этом базисе оператор g матрицей diag 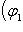
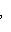

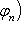 и обозначим через A матрицу оператора g в исходном базисе. Очевидно, exp(ig) = f и exp(iA) = U.
и обозначим через A матрицу оператора g в исходном базисе. Очевидно, exp(ig) = f и exp(iA) = U.