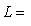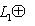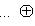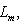Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Теоремы классификации / 1 2 3 4 5 6 7 8 9 10 11 12 13
Доказательство. а) Пусть
С другой стороны, из невырожденности L0 следует, что б) Из определений ясно, что
Это завершает доказательство. 3. Теорема. Пусть (L, g) - конечномерное ортогональное (над полем характеристики
одномерных в ортогональном и эрмитовом случае и одномерных вырожденных или двумерных невырожденных в симплектическом случае. -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
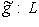
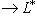 (или
(или 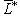 ) - отображение, ассоциированное с g, как в предыдущем параграфе. Обозначим через
) - отображение, ассоциированное с g, как в предыдущем параграфе. Обозначим через 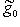 его ограничение на
его ограничение на 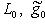
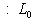
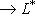 (или
(или 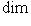
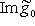
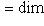
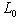 . Это означает, что когда l0 пробегает L0, линейные формы
. Это означает, что когда l0 пробегает L0, линейные формы 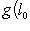
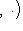 от второго аргумента из L или
от второго аргумента из L или 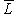 пробегают dim L0-мерное пространство линейных форм на L или
пробегают dim L0-мерное пространство линейных форм на L или 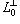 есть пересечение ядер этих форм,
есть пересечение ядер этих форм, 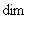
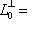
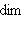
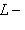
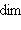
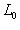 , т. е.
, т. е.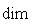
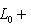
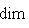
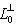
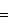
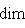
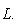
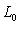
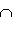
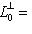
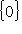 , т. к.
, т. к. 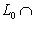
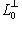 есть ядро органичения g на L0. Поэтому сумма
есть ядро органичения g на L0. Поэтому сумма 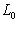
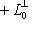 прямая; но ее размерность равна dim L, так что
прямая; но ее размерность равна dim L, так что 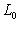
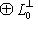
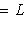 .
.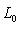
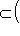
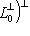 . С другой стороны, если
. С другой стороны, если 
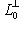 невырождены, то по предыдущему
невырождены, то по предыдущему
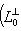
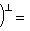
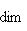
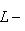
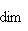
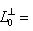
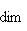
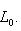
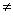
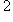 ), эрмитово или симплектическое пространство. Тогда существует разложение L в прямую сумму попарно ортогональных подпространств:
), эрмитово или симплектическое пространство. Тогда существует разложение L в прямую сумму попарно ортогональных подпространств: