Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Теоремы классификации / 1 2 3 4 5 6 7 8 9 10 11 12 13
б) Всякую квадратную антисимметричную матрицу G над полем
Число 2r равно рангу G. в) Всякую эрмитову матрицу G над C можно привести к диагональному виду с числами 8. Билинейные формы. Если векторы пространства (L, g) с фиксированным базисом записываются координатами в этом базисе, то выражение g через координаты является билинейной формой от 2n переменных, n = dim L:
где G - матрица Грама базиса. Замена базиса сводится к линейному преобразованию переменных x1, ..., xn и y1, ..., yn с помощью одной и той же невырожденной матрицы A в билинейном случае (или матрицы A для -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
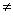
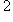 можно привести преобразованием
можно привести преобразованием 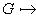
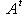
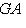 , где A невырождена, к виду
, где A невырождена, к виду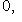
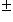
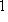 на диагонали преобразованием
на диагонали преобразованием 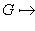
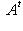
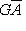 , где A невырождена. Количества 0 и
, где A невырождена. Количества 0 и 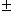
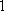 зависят лишь от G.
зависят лишь от G.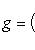
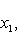
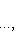
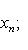
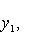
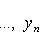
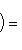
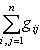
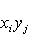
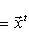
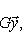
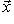 , для
, для  и
и  в полуторалинейном случае). Предыдущие результаты означают, что в зависимости от свойств симметрии матрицы G форму можно привести таким преобразованием к одному из следующих видов, называемых каноническими.
в полуторалинейном случае). Предыдущие результаты означают, что в зависимости от свойств симметрии матрицы G форму можно привести таким преобразованием к одному из следующих видов, называемых каноническими.