Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Самосопряженные операторы1. В части Линейные пространства и линейные отображения мы видели, что простейший и наиболее важный класс линейных операторов образуют диагонализируемые операторы. Оказывается, что в евклидовых и унитарных пространствах совершенно особую роль играют операторы с вещественным спектром, диагонализируемые в некотором ортонормированном базисе. Иными словами, эти операторы осуществляют вещественные растяжения пространства вдоль системы попарно ортогональных направлений. Пусть {e1, ..., en} - ортонормированный базис в L и (f(l1), l2) = (l1, f(l2)) для всех Действительно,
(в унитарном случае вещественность -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

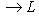 - оператор, для которого
- оператор, для которого 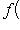
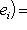
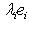
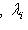
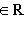 , i = 1, ..., n. Нетрудно убедиться, что он обладает следующим простым свойством:
, i = 1, ..., n. Нетрудно убедиться, что он обладает следующим простым свойством: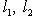
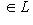 . (1)
. (1)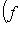
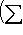
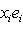
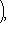
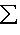
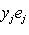
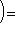
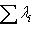
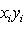 или
или 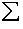
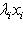
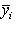 ,
,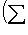
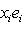
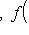
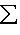
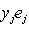
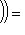
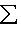
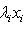
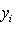 или
или 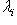 использовалась во второй формуле). Операторы со свойством (1) называются самосопряженными, и мы установили, что операторы с вещественным спектром, диагонализируемые в ортонормированном базисе, самосопряжены. Вскоре докажем и обратное утверждение, но сначала исследуем свойство самосопряженности более систематично.
использовалась во второй формуле). Операторы со свойством (1) называются самосопряженными, и мы установили, что операторы с вещественным спектром, диагонализируемые в ортонормированном базисе, самосопряжены. Вскоре докажем и обратное утверждение, но сначала исследуем свойство самосопряженности более систематично.