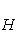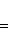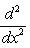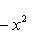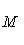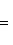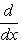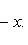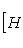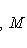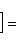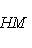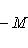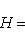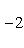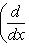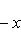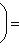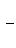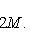Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Разумеется, самосопряженность на этом пространстве можно было бы проверить и непосредственным интегрированием по частям: член типа в) Многочлен Эрмита
Функция
с собственным значением -(2n + 1). Первое утверждение проверяется прямой индукцией по n, которую мы опускаем. Для доказательства второго утверждения рассмотрим вспомогательный оператор
Легко проверить, что
-1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
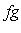
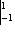 пропадет здесь из-за множителя x2 - 1 в коэффициентах оператора. Тогда из результатов этого пункта и теоремы п. 4 получается другое доказательство попарной ортогональности многочленов Лежандра.
пропадет здесь из-за множителя x2 - 1 в коэффициентах оператора. Тогда из результатов этого пункта и теоремы п. 4 получается другое доказательство попарной ортогональности многочленов Лежандра.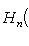
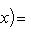
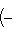
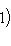
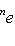

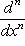
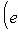
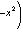 есть собственный вектор с собственным значением -2n оператора
есть собственный вектор с собственным значением -2n оператора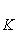
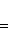
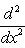
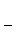
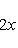
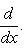
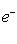
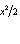
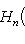
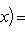
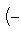
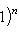
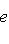
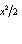
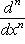
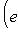
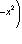 является собственным вектором оператора
является собственным вектором оператора