Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
б) Многочлены Лежандра. Оператор
формально самосопряжен и переводит пространство многочленов степени
откуда по формуле Лейбница, примененной к обеим частям,
Разделив последнее равенство на 2nn! и вспомнив определение многочленов Лежандра, получим отсюда
Таким образом, оператор -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
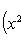

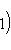
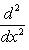
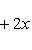
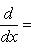
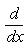
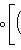
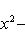
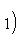
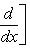
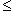
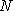 в себя. Имеет место очевидное тождество
в себя. Имеет место очевидное тождество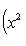
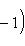
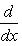
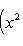
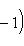

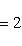
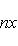
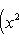
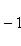
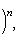
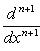
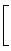
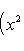
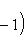
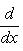
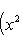
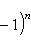
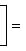
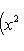
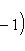
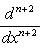
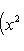
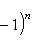
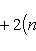
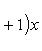
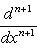

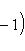
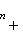

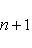
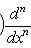
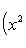
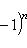
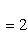
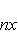
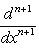
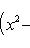
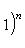
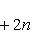
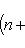
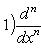
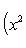
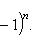
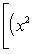
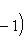
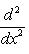
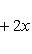
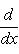
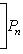
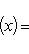
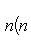
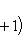
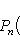
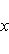
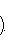
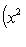
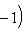
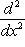
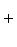
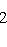
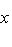
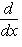 на пространстве многочленов степени
на пространстве многочленов степени