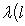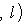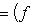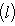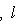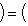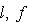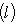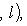Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
в евклидовом случае, и аналогично
в унитарном. Следовательно, если оператор f самосопряжен, то построенная по нему новая метрика (l1, l2)f будет по-прежнему симметричной или эрмитовой. Верно и обратное, как нетрудно убедиться прямо или с помощью предложения п. 3. Таким образом, установили биекцию между множествами самосопряженных операторов, с одной стороны, и симметричных скалярных произведений в пространстве, где одно невырожденное скалярное произведение задано, - с другой. В евклидовом и унитарном случае после выбора ортонормированного базиса соответствие легко описывается на матричном языке: матрица Грама ( , )f транспонирована к матрице отображения f. Теперь докажем основную теорему о самосопряженных операторах, параллельную теореме п. 4 об ортогональных и унитарных операторах и тесно с ней связанную. 5. Теорема. а) Для того чтобы оператор f в конечномерном евклидовом или унитарном пространстве был самосопряжен, необходимо и достаточно, чтобы он диагонализировался в ортонормированном базисе и имел вещественный спектр. б) Собственные векторы самосопряженного оператора, отвечающие разным собственным значениям, ортогональны. Доказательство. а) Достаточность провели в начале этого раздела. Вещественность спектра в унитарном случае устанавливается просто: пусть
-1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
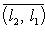
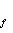
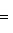
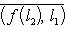
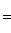

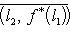


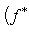
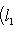
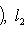
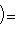
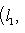
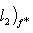
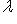 - собственное значение оператора
- собственное значение оператора 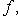
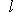
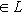 - соответствующий собственный вектор. Тогда
- соответствующий собственный вектор. Тогда