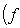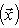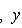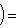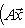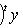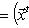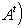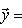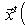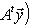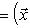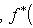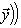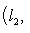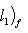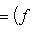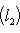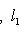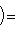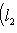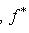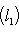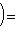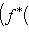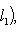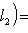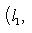Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Операторы 3. Предложение. Если оператор В частности, оператор самосопряжен тогда и только тогда, когда его матрица в ортонормированном базисе симметрична или эрмитова. Доказательство. Обозначая скалярное произведение в L скобками, а векторы - столбцами их координат в ортонормированном базисе, имеем
(евклидов случай). Отсюда и следует, что матрица f* равна At. Унитарный случай разбирается аналогично. 4. Самосопряженные операторы и скалярные произведения. Пусть L - пространство с симметричным или эрмитовым скалярным произведением ( , ). Для любого линейного оператора (l1, l2)f = (f(l1), l2). Предположим, что L невырождено, так что можем пользоваться понятием сопряженного оператора. Тогда
-1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

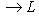 со свойством f* = f в евклидовых и конечномерных унитарных пространствах называются самосопряженными, в евклидовом случае - также симметричными, а в унитарном - эрмитовыми. Эта терминология объясняется следующим простым замечанием.
со свойством f* = f в евклидовых и конечномерных унитарных пространствах называются самосопряженными, в евклидовом случае - также симметричными, а в унитарном - эрмитовыми. Эта терминология объясняется следующим простым замечанием.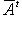 (унитарный случай).
(унитарный случай).