Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
10. Формально сопряженные дифференциальные операторы. Рассмотрим какое-нибудь пространство вещественных функций на отрезке [a, b] со скалярным произведением
Предположим, что оператор
Поэтому, если пространство состоит только из функций, принимающих на концах интервала одинаковые значения, то
т. е. на таком пространстве оператор Используя формулу интегрирования по частям несколько раз или пользуясь формальным операторным соотношением
где запись -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
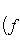
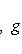
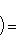
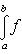
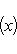
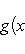
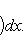
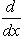 переводит его в себя. Согласно формуле интегрирования по частям
переводит его в себя. Согласно формуле интегрирования по частям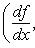
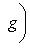
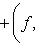
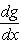
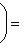
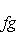
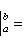
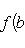
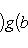
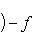
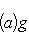
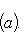
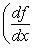
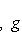
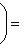
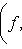
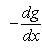
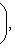

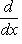 сопряжен с оператором
сопряжен с оператором 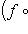
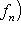
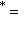
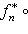
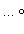
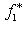 , получаем, что на таких пространствах
, получаем, что на таких пространствах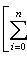
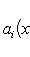
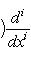
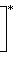
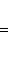
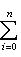
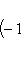
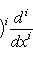
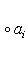

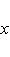
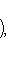 (3)
(3)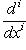
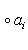
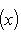 для оператора означает, что, применяя его к функции f(x), сначала умножаем ее на ai(x) и затем дифференцируем i раз по x.
для оператора означает, что, применяя его к функции f(x), сначала умножаем ее на ai(x) и затем дифференцируем i раз по x.