Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2. Сопряженные операторы в пространствах с билинейной формой. В части Линейные пространства и линейные отображения показали, что для любого линейного отображения (f*(m*), l) = (m*, f(l)), где В частности, при M = L оператору g(f*(l), m) = g(l, f(m)). Он по-прежнему называется сопряженным с f (относительно скалярного произведения g). В полуторалинейном случае g(f*(l), m) = g(l, f(m)). Операция -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
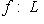
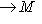 существует единственное линейное отображение
существует единственное линейное отображение 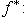
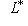
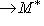 , для которого
, для которого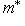
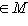

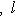
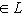 и где скобки означают канонические билинейные отображения
и где скобки означают канонические билинейные отображения 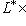
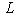
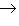
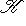
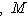
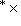
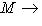
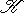 .
.
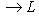 отвечает оператор
отвечает оператор 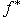
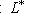
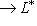 . Предположим теперь, что на L имеется невырожденная билинейная форма
. Предположим теперь, что на L имеется невырожденная билинейная форма 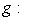
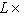
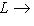
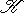 , определяющая изоморфизм
, определяющая изоморфизм 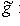
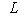
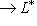 . Тогда, отождествив L* с L посредством
. Тогда, отождествив L* с L посредством 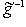 , можем рассмотреть f*, точнее
, можем рассмотреть f*, точнее 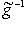
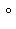
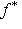
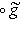 , как оператор на L. По-прежнему будем обозначать его f* (точнее было бы писать, например,
, как оператор на L. По-прежнему будем обозначать его f* (точнее было бы писать, например, 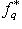 но f* в старом смысле в этом разделе больше не будет фигурировать). Очевидно, новый оператор f* однозначно определяется формулой
но f* в старом смысле в этом разделе больше не будет фигурировать). Очевидно, новый оператор f* однозначно определяется формулой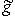 определяет изоморфизм L с
определяет изоморфизм L с 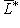 , а не с L*. Поэтому на L с помощью этого изоморфизма следует переносить оператор
, а не с L*. Поэтому на L с помощью этого изоморфизма следует переносить оператор 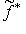
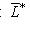
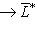 , который определяется как
, который определяется как 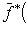
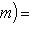
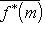 . Перенесенный оператор
. Перенесенный оператор 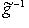
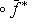
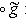
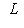
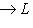 линеен. Следовало бы обозначить его f+, но сохраним более традиционное обозначение f*. Тогда и в полуторалинейном случае будет справедлива формула
линеен. Следовало бы обозначить его f+, но сохраним более традиционное обозначение f*. Тогда и в полуторалинейном случае будет справедлива формула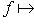
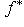 линейна, если g билинейна, и антилинейна, если g полуторалинейна.
линейна, если g билинейна, и антилинейна, если g полуторалинейна.