Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Далее, если самосопряженный оператор f диагонализируется в ортонормированном базисе
Эта формула называется спектральным разложением оператора f. Можно считать, что Теорема п. 5 обобщается также на ограниченные по норме (и, с осложнениями, на неограниченные) самосопряженные операторы в бесконечномерных гильбертовых пространствах. Однако это обобщение требует очень нетривиального изменения некоторых основных понятий. Главные проблемы связаны со структурой спектра: в конечномерном случае Ограничимся описанием нескольких важных принципов на примерах, где эти затруднения не возникают. -1-2-3-4-5-6-7-8-9-10-11-12-13-14- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
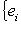
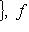
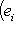
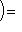
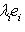 и pi - ортогональный проектор L на подпространство, натянутое на ei, то
и pi - ортогональный проектор L на подпространство, натянутое на ei, то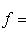
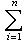
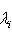
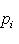 (2)
(2)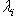 пробегает только попарно различные собственные значения, а pi есть оператор ортогонального проектирования на полное корневое подпространство
пробегает только попарно различные собственные значения, а pi есть оператор ортогонального проектирования на полное корневое подпространство 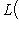
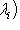 ; формула (2) останется верной.
; формула (2) останется верной.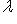 является собственным значением f тогда и только тогда, когда оператор
является собственным значением f тогда и только тогда, когда оператор 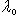 собственных векторов, вообще говоря, нет. С другой стороны, именно множество точек необратимости оператора
собственных векторов, вообще говоря, нет. С другой стороны, именно множество точек необратимости оператора