Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Скалярные произведения / 1 2 3 4 5 6 7 8 9 10 11
Действительно, если
что доказывает требуемое. Здесь мы пользовались замечанием, сделанным в параграфе Двойственность, о том, что каноническое отображение 3. Свойства симметрии скалярных произведений. Перестановка аргументов в билинейном скалярном произведении g определяет новое скалярное произведение gt: gt(l, m) = g(m, l). В полуторалинейном случае эта операция также меняет места "линейного" и "полулинейного" аргументов; если мы хотим, чтобы этого не произошло, то удобнее рассматривать
У |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
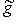 задано матрицей Gt, то соответствующее скалярное произведение g в двойственных базисах имеет вид
задано матрицей Gt, то соответствующее скалярное произведение g в двойственных базисах имеет вид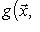
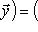
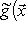
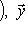
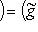
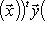 или
или 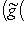
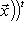
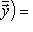
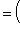
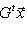
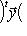 или
или 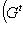
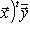
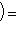
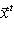
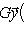 или
или 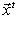
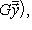
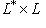
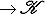 в двойственных базисах определяется формулой
в двойственных базисах определяется формулой 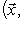
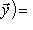
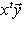 .
.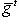 :
: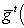
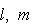
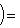
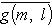

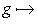
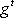 или
или 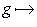
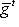 легко описывается на языке матриц Грама: она отвечает операции
легко описывается на языке матриц Грама: она отвечает операции 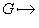
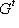 или
или 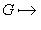
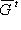 соответственно (предполагается, что
соответственно (предполагается, что 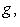
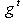
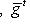 пишутся в одном и том же базисе L).
пишутся в одном и том же базисе L).