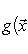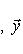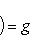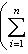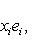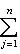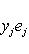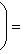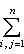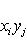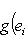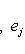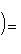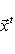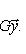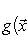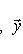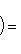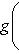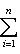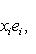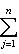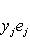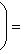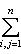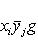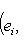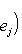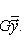Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Скалярные произведения / 1 2 3 4 5 6 7 8 9 10 11
Общие полилинейные отображения будут рассмотрены в разделе, посвященном тензорной алгебре. В данном разделе займемся важнейшим для приложений классом билинейных функций Скалярное произведение 2. Способы задания скалярного произведения. а) Пусть G = (g(ei, ej)); i, j = 1, ..., n. Она называется матрицей Грама базиса {e1, ..., en} относительно g, а также матрицей g в базисе {e1, ..., en}. Задание {ei} и G вполне определяет g, потому что в силу свойства билинейности
В случае полуторалинейной формы аналогичная формула приобретает вид
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
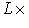
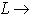
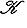 , а также, при
, а также, при 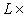
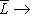
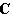 , где
, где 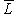 - пространство, комплексно сопряженное с L (см.
- пространство, комплексно сопряженное с L (см. 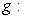
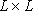
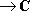 , линейное по первому агрументу и полулинейное по второму:
, линейное по первому агрументу и полулинейное по второму: 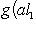
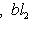
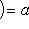
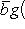
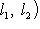 .
.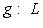
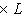
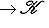 (или
(или