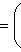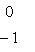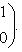Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Скалярные произведения / 1 2 3 4 5 6 7 8 9 10 11
Ясно поэтому, что одномерные симплектические пространства не могут быть строительным материалом для конструкции общих симплектических пространств, и нужно пойти по крайней мере на шаг дальше. 10. Двумерные симплектические пространства. Пусть (L, g) - двумерное пространство с кососимметрической формой g над полем g(al + a'l', bl + b'l') = abg(l, l) + ab'g(l, l') - a'bg(l, l') + bb'g(l', l') = 0. Пусть теперь g ненулевая и, значит, невырожденная. Тогда существует пара векторов e1, e2 с Пусть g(e1, e2) = 1. Тогда векторы e1, e2 линейно независимы и, значит, образуют базис L: если, скажем, e1 = ae2, то g(ae2, e2) = ag(e2, e2) = 0. В координатах относительно такого базиса скалярное произведение g записывается в виде g(x1e1 + x2e2, y1e1 + y2e2) = x1y2 - x2y1 и имеет матрицу Грама
Окончательно, получаем: Над полем |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
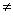
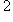 . Если форма g вырождена, то она автоматически нулевая. В самом деле, пусть
. Если форма g вырождена, то она автоматически нулевая. В самом деле, пусть 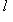
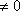 - такой вектор, что g(l, m) = 0, для всех
- такой вектор, что g(l, m) = 0, для всех 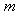
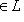 . Дополним l до базиса {l, l'} в L и учтем, что g(l', l') = g(l, l) = 0 по предыдущему пункту. Тогда для любых
. Дополним l до базиса {l, l'} в L и учтем, что g(l', l') = g(l, l) = 0 по предыдущему пункту. Тогда для любых 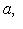
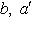
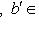
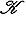 имеем
имеем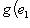
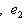
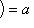
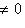 и даже с a = 1: g(a -1e1, e2) = a -1a = 1.
и даже с a = 1: g(a -1e1, e2) = a -1a = 1.