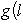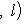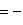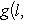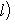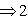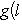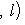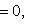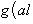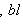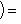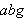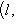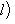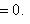Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Скалярные произведения / 1 2 3 4 5 6 7 8 9 10 11
На групповом языке это определяет прямое разложение Над C любое одномерное эрмитово пространство изометрично одномерному координатному пространству с одним из трех скалярных произведений: Одномерные ортогональные пространства R (или эрмитовы над C) со скалярными произведениями xy, -xy, 0 (или 9. Одномерные симплектические пространства. Здесь мы встречаемся с новой ситуацией: любая антисимметричная форма на одномерном пространстве над полем характеристики
Что касается характеристики 2, то условие антисимметрии g(l, m) = - g(m, l) в этом случае равносильно условию симметрии g(l, m) = g(m, l), так что над такими полями симплектическая геометрия не отличается от ортогональной. Впрочем, у ортогональной геометрии также появляются свои особенности, и мы обычно будем этот случай исключать из рассмотрения. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
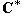
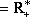
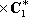 и изоморфизм
и изоморфизм 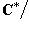
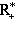
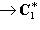 . Таким образом, невырожденные полуторалинейные формы классифицируются комплексными числами, по модулю равными единице. Однако мы еще не полностью учли свойства эрмитовости, которое означает, что
. Таким образом, невырожденные полуторалинейные формы классифицируются комплексными числами, по модулю равными единице. Однако мы еще не полностью учли свойства эрмитовости, которое означает, что 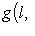
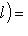
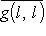 , т. е. что значения g(l, l) все вещественны. Поэтому эрмитовым формам отвечают только числа
, т. е. что значения g(l, l) все вещественны. Поэтому эрмитовым формам отвечают только числа 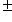
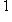 в
в 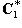 , как и в ортогональном случае над R. Окончательный ответ:
, как и в ортогональном случае над R. Окончательный ответ: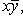
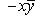
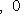 .
.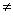
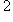 тождественно равна нулю, в частности, вырождена! Действительно,
тождественно равна нулю, в частности, вырождена! Действительно,