Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Скалярные произведения / 1 2 3 4 5 6 7 8 9 10 11
Очевидно, ядро формы g совпадает с ядром линейного отображения
и потому является линейным подпространством в L. Поэтому задание невырожденной формы g можно заменить заданием изоморфизма Ранг g определяется как размерность образа 6. Задача классификации. Пусть (L1, g1), (L2, g2) - два линейных пространства со скалярными произведениями над полем g1(l, l') = g2(f(l), f(l')) для всех Назовем такие пространства изометричными, если между ними существует изометрия. Очевидно, тождественное отображение является изометрией, композиция изометрий есть изометрия и линейное отображение, обратное к изометрии, есть изометрия. В следующем параграфе мы решим задачу классификации пространств с точностью до изометрии, а затем изучим группы изометрий пространства с самим собой и покажем, что среди них содержатся классические группы, описанные в разделе Матрицы. Классическое решение задачи классификации состоит в том, что всякое пространство со скалярным произведением разлагается в прямую сумму попарно ортогональных подпространств малой размерности (один в ортогональном и эрмитовом случае, один или два - в симплектическом). Поэтому мы закончим этот параграф непосредственным описанием таких маломерных пространств с метрикой. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
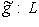
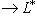 (или
(или 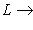
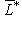 )
)
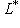 (или
(или 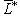 ). Так как матрицей
). Так как матрицей 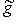 служит транспонированная матрица Грама Gt базиса L, невырожденность g равносильна невырожденности матрицы Грама (любого базиса). В тензорной алгебре и ее приложениях к дифференциальной геометрии и физике очень широко используется то обстоятельство, что невырожденная ортогональная форма g определяет изоморфизм
служит транспонированная матрица Грама Gt базиса L, невырожденность g равносильна невырожденности матрицы Грама (любого базиса). В тензорной алгебре и ее приложениях к дифференциальной геометрии и физике очень широко используется то обстоятельство, что невырожденная ортогональная форма g определяет изоморфизм 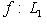
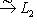 , который сохраняет значения всех скалярных произведений, т. е.
, который сохраняет значения всех скалярных произведений, т. е.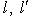
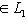 .
.