Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Скалярные произведения / 1 2 3 4 5 6 7 8 9 10 11
Геометрические свойства скалярных произведений, отличающихся друг от друга лишь множителем, практически одни и те же. Напротив, ортогональная геометрия во многом отличается от симплектической: редукция соотношения gt = g и gt = - g друг к другу таким простым способом невозможна. 4. Ортогональность. Пусть (L, g) - векторное пространство со скалярным произведением. Векторы
и аналогично в эрмитовом случае. Если не оговорено обратное, в дальнейшем будем рассматривать только ортогональные, симплектические или эрмитовы скалярные произведения. Первое применение понятия ортогональности содержится в следующем определении. 5. Определение. а) Ядром скалярного произведения g на пространстве L называется множество всех векторов б) g называется невырожденным, если ядро формы g тривиально, т. е. состоит только из нуля. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
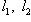
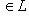 называются ортогональными (относительно g), если g(l1, l2) = 0. Подпространства
называются ортогональными (относительно g), если g(l1, l2) = 0. Подпространства 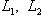
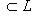 называются ортогональными, если g(l1, l2) = 0 для всех
называются ортогональными, если g(l1, l2) = 0 для всех 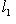
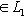
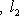
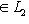 . Основная причина, по которой важны лишь скалярные произведения с одним из свойств симметрии предыдущего пункта, состоит в том, что для них свойство ортогональности векторов или подпространств симметрично относительно этих векторов или подпространств. Действительно: если
. Основная причина, по которой важны лишь скалярные произведения с одним из свойств симметрии предыдущего пункта, состоит в том, что для них свойство ортогональности векторов или подпространств симметрично относительно этих векторов или подпространств. Действительно: если 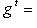
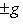 или
или 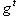
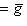 , то
, то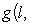
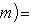
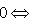
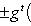
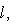
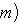
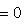
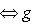
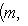
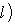
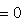
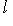
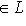 , ортогональных ко всем векторам L.
, ортогональных ко всем векторам L.