Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Пространство Минковского / 1 2 3 4 5 6 7 8 9 10 11 12 13
Далее, в качестве ft(e1, e2, e3) выберем ортонормированный базис в Обозначим через 11. Теорема. Группа Лоренца Тождественное отображение лежит, очевидно, в 12. Теорема. Реализуем
Отображение s определяет сюръективный гомоморфизм SL(2, C) на -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
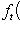
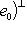 , получающийся из проекции {e1, e2, e3} на
, получающийся из проекции {e1, e2, e3} на 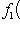
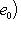
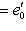 , а {f1(e1), f1(e2), f1(e3)} и
, а {f1(e1), f1(e2), f1(e3)} и 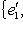
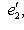
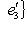 суть одинаково ориентированные ортонормированные базисы в
суть одинаково ориентированные ортонормированные базисы в 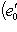
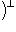 . Их можно перевести друг в друга непрерывным семейством чисто евклидовых вращений
. Их можно перевести друг в друга непрерывным семейством чисто евклидовых вращений 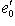 неподвижным. Это завершает доказательство.
неподвижным. Это завершает доказательство.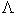 группу Лоренца, т. е. группу изометрий пространства
группу Лоренца, т. е. группу изометрий пространства  , или О(1, 3). Пусть далее
, или О(1, 3). Пусть далее 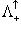 - подгруппа
- подгруппа 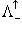 - подмножество
- подмножество 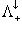 - подмножество
- подмножество 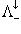 - подмножество
- подмножество 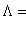
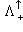
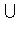
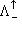
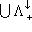
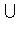
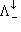 .
.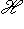 в базисе {h1, h2}. Для любой матрицы
в базисе {h1, h2}. Для любой матрицы 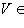
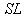
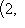
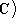 поставим в соответствие матрице
поставим в соответствие матрице 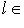
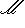 новую матрицу
новую матрицу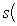
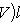
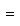
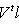
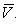
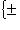
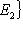 .
.