Геометрия пространств со скалярным произведением / Самосопряженные операторы в квантовой механике / 1 2 3 4 5 6 7 8 9 10 11 12 13
В примере г) п. 4 был написан гамильтониан квантового осциллятора: 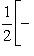 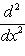 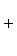 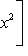 . В разделе в) п. 10 было показано, что функции . В разделе в) п. 10 было показано, что функции 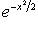 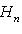 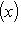 образуют систему стационарных состояний гармонического осциллятора с уровнями энергии образуют систему стационарных состояний гармонического осциллятора с уровнями энергии 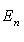 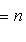 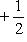 , n = 1, 2, 3, ... (Более подробный анализ показывает, что энергия измеряется здесь в единицах , n = 1, 2, 3, ... (Более подробный анализ показывает, что энергия измеряется здесь в единицах 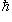 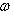 , где константа , где константа 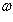 отвечает частоте колебаний соответствующего классического осциллятора.) Разумным образом определив унитарное пространство, в котором следует работать, можно показать, что это полная система стационарных состояний. При n > 0 осциллятор может излучить порцию энергии отвечает частоте колебаний соответствующего классического осциллятора.) Разумным образом определив унитарное пространство, в котором следует работать, можно показать, что это полная система стационарных состояний. При n > 0 осциллятор может излучить порцию энергии 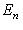 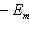 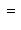 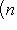 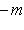 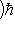 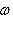 и перейти из состояния и перейти из состояния 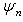 в состояние в состояние 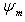 . В применении к квантовой теории электромагнитного поля об этом говорят как об "излучении n - m фотонов частоты . В применении к квантовой теории электромагнитного поля об этом говорят как об "излучении n - m фотонов частоты 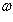 ". Обратный процесс будет поглощением n - m фотонов; при этом осциллятор перейдет в более высокое (возбужденное) состояние. Важно, что энергия может быть получена или передана лишь целыми кратными ". Обратный процесс будет поглощением n - m фотонов; при этом осциллятор перейдет в более высокое (возбужденное) состояние. Важно, что энергия может быть получена или передана лишь целыми кратными 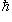 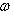 . .
В основном состоянии осциллятор имеет ненулевую энергию 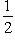 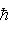 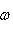 , которая, однако, никак не может быть передана - более низких энергетических состояний осциллятор не имеет. Электромагнитное поле в квантовых моделях рассматривается как суперпозиция бесконечно многих осцилляторов (отвечающих, в частности, разным частотам , которая, однако, никак не может быть передана - более низких энергетических состояний осциллятор не имеет. Электромагнитное поле в квантовых моделях рассматривается как суперпозиция бесконечно многих осцилляторов (отвечающих, в частности, разным частотам 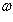 ). В основном состоянии - вакууме - оказывается поэтому, что поле имеет бесконечную энергию, хотя с классической точки зрения оно является нулевым - раз от него нельзя отнять энергию, оно не может ни на что воздействовать! Это простейшая модель глубоких трудностей современной квантовой теории поля. Ни математический аппарат, ни физическая интерпретация квантовой теории поля не достигли какой-либо степени законченности. Это открытая и увлекательная наука. ). В основном состоянии - вакууме - оказывается поэтому, что поле имеет бесконечную энергию, хотя с классической точки зрения оно является нулевым - раз от него нельзя отнять энергию, оно не может ни на что воздействовать! Это простейшая модель глубоких трудностей современной квантовой теории поля. Ни математический аппарат, ни физическая интерпретация квантовой теории поля не достигли какой-либо степени законченности. Это открытая и увлекательная наука.
7. Формулы теории возмущений. В аппарате квантовой механики важную роль играют ситуации, когда гамильтониан H системы может рассматриваться как сумма 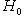 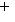 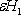 , где H0 - "невозмущенный" гамильтониан, а , где H0 - "невозмущенный" гамильтониан, а 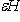 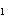 - малая добавка, "возмущение". С физической точки зрения возмущение часто обусловливает взаимодействие системы с "внешним миром" (например, внешним магнитным полем) или компонент системы между собой (тогда H0 отвечает идеализированному случаю системы, состоящей из свободных, невзаимодействующих компонент). С математической точки зрения такое представление оправдано, когда спектральный анализ невозмущенного гамильтониана H0 проще, чем H, и спектральные характеристики H удобно представлять рядами по степеням - малая добавка, "возмущение". С физической точки зрения возмущение часто обусловливает взаимодействие системы с "внешним миром" (например, внешним магнитным полем) или компонент системы между собой (тогда H0 отвечает идеализированному случаю системы, состоящей из свободных, невзаимодействующих компонент). С математической точки зрения такое представление оправдано, когда спектральный анализ невозмущенного гамильтониана H0 проще, чем H, и спектральные характеристики H удобно представлять рядами по степеням 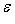 , первые члены которых определяются через H0. Ограничимся следующими наиболее употребительными формулами и качественными замечаниями к ним. , первые члены которых определяются через H0. Ограничимся следующими наиболее употребительными формулами и качественными замечаниями к ним.
-1-2-3-4-5-6-7-8-9-10-11-12-13-
|
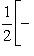
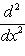
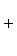
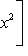 . В разделе в)
. В разделе в) 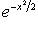
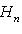
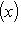 образуют систему стационарных состояний гармонического осциллятора с уровнями энергии
образуют систему стационарных состояний гармонического осциллятора с уровнями энергии 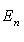
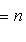
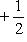 , n = 1, 2, 3, ... (Более подробный анализ показывает, что энергия измеряется здесь в единицах
, n = 1, 2, 3, ... (Более подробный анализ показывает, что энергия измеряется здесь в единицах 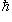
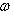 , где константа
, где константа 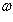 отвечает частоте колебаний соответствующего классического осциллятора.) Разумным образом определив унитарное пространство, в котором следует работать, можно показать, что это полная система стационарных состояний. При n > 0 осциллятор может излучить порцию энергии
отвечает частоте колебаний соответствующего классического осциллятора.) Разумным образом определив унитарное пространство, в котором следует работать, можно показать, что это полная система стационарных состояний. При n > 0 осциллятор может излучить порцию энергии 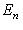
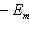
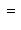
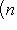
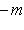
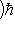
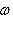 и перейти из состояния
и перейти из состояния 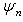 в состояние
в состояние 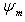 . В применении к квантовой теории электромагнитного поля об этом говорят как об "излучении n - m фотонов частоты
. В применении к квантовой теории электромагнитного поля об этом говорят как об "излучении n - m фотонов частоты 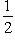
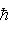
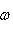 , которая, однако, никак не может быть передана - более низких энергетических состояний осциллятор не имеет. Электромагнитное поле в квантовых моделях рассматривается как суперпозиция бесконечно многих осцилляторов (отвечающих, в частности, разным частотам
, которая, однако, никак не может быть передана - более низких энергетических состояний осциллятор не имеет. Электромагнитное поле в квантовых моделях рассматривается как суперпозиция бесконечно многих осцилляторов (отвечающих, в частности, разным частотам 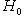
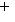
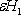 , где H0 - "невозмущенный" гамильтониан, а
, где H0 - "невозмущенный" гамильтониан, а 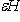
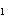 - малая добавка, "возмущение". С физической точки зрения возмущение часто обусловливает взаимодействие системы с "внешним миром" (например, внешним магнитным полем) или компонент системы между собой (тогда H0 отвечает идеализированному случаю системы, состоящей из свободных, невзаимодействующих компонент). С математической точки зрения такое представление оправдано, когда спектральный анализ невозмущенного гамильтониана H0 проще, чем H, и спектральные характеристики H удобно представлять рядами по степеням
- малая добавка, "возмущение". С физической точки зрения возмущение часто обусловливает взаимодействие системы с "внешним миром" (например, внешним магнитным полем) или компонент системы между собой (тогда H0 отвечает идеализированному случаю системы, состоящей из свободных, невзаимодействующих компонент). С математической точки зрения такое представление оправдано, когда спектральный анализ невозмущенного гамильтониана H0 проще, чем H, и спектральные характеристики H удобно представлять рядами по степеням 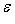 , первые члены которых определяются через H0. Ограничимся следующими наиболее употребительными формулами и качественными замечаниями к ним.
, первые члены которых определяются через H0. Ограничимся следующими наиболее употребительными формулами и качественными замечаниями к ним.