Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы в квантовой механике / 1 2 3 4 5 6 7 8 9 10 11 12 13
Так как в силу теоремы п. 4
интерпретируется тогда как утверждение о том, что, производя измерения f на любом состоянии Физические величины, о которых говорили выше, и соответствующие им самосопряженные операторы также называют наблюдаемыми. Постулат о наблюдаемых иногда трактуется более широко и считается, что любому самосопряженному оператору отвечает некоторая физическая наблюдаемая. В бесконечномерных пространствах
Кроме того, в бесконечномерном случае операторы наблюдаемых могут оказаться определенными лишь на некотором подпространстве -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
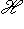 разлагается в ортогональную прямую сумму
разлагается в ортогональную прямую сумму 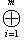
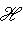
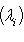
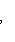
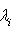
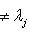 при
при 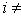
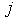 , можем разложить
, можем разложить  в соответствующую сумму проекций
в соответствующую сумму проекций 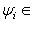
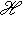
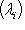 , i = 1, ..., m. Теорема Пифагора
, i = 1, ..., m. Теорема Пифагора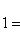
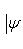

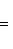
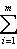
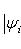
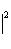
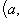
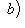
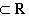 . Этому интервалу также можно поставить в соответствие подпространство
. Этому интервалу также можно поставить в соответствие подпространство 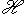
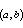
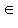
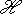 - образ ортогонального проектора p(a, b) на
- образ ортогонального проектора p(a, b) на 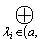
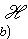
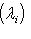 в конечномерном случае, - и искомая вероятность равна
в конечномерном случае, - и искомая вероятность равна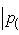
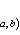
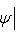
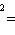
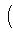
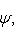
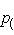
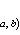
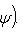
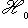
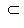
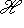 .
.