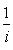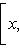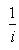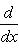Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Самосопряженные операторы в квантовой механике / 1 2 3 4 5 6 7 8 9 10 11 12 13
Это показывает, что средний разброс значений некоммутирующих наблюдаемых f, g, вообще говоря, не может быть одновременно сделан как угодно малым. Говорят еще, что некоммутирующие наблюдаемые не измеримы одновременно; к этой формулировке следует относиться с теми же предосторожностями, что и к термину "измерение". Особую роль играет применение неравенства Гейзенберга к случаю канонически сопряженных пар наблюдаемых, которые по определению удовлетворяют соотношению
каково бы ни было состояние
Эти операторы появляются в квантовых моделях физических систем, которые на классическом языке называются "частица, движущаяся в одномерном потенциальном поле". Опишем эти и некоторые другие наблюдаемые подробнее. -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
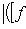
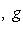
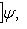
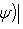
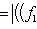
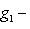
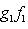
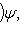
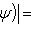
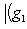
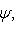
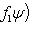
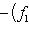
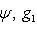
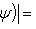
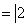
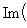
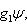
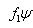
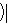

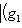
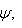
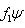
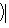
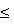
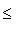
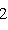

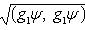



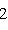
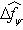
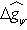

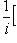
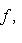
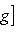
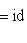 . Для них
. Для них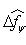

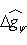
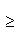
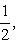
 . Заметим, что в конечномерных пространствах таких пар нет, т. к. Tr [f, g] = 0, Tr id = dim
. Заметим, что в конечномерных пространствах таких пар нет, т. к. Tr [f, g] = 0, Tr id = dim 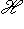 . Однако в бесконечномерных пространствах они существуют. Классический пример:
. Однако в бесконечномерных пространствах они существуют. Классический пример: