Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Унитарные пространства / 1 2 3 4 5 6 7 8 9 10 11
Доказательство. Условие эрмитовой симметрии a(l, m) + ib(l, m) = a(m, l) - ib(m, l), т. е. симметрии a и антисимметрии b. Условие a(il, m) + ib(il, m) = g(il, m) = ig(l, m) = - b(l, m) + ia(l, m), откуда следуют соотношения б) и утверждение в). Наконец, g(l, l) = a(l, l) в силу антисимметрии b, откуда следует г). 3. Следствие. В прежних обозначениях, если g положительно определена и {e1, ..., en} - ортонормированный базис для g, то {e1, ..., en, ie1, ..., ien} является ортонормированным базисом для a и симплектическим для b. Наоборот, если L - 2n-мерное вещественное пространство с евклидовой формой a и симплектической b, а также базисом {e1, ..., en, en+1, ..., e2n}, ортонормированным для a и симплектическим для b, то, введя на L комплексную структуру с помощью оператора
и скалярное произведение g(l, m) = a(l, m) + ib(l, m), получим комплексное пространство с положительно определенной эрмитовой формой, для которого {e1, ..., en} является ортонормированным базисом над C. Доказательство получается простой проверкой с помощью предложения п. 2. Вернемся теперь к унитарным пространствам L. Комплексное неравенство Коши-Буняковского-Шварца имеет следующий вид: |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник


 равносильно тому, что
равносильно тому, что




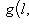
 равносильно i-инвариантности a и b. Условие C-линейности g по первому аргументу означает R-линейность и линейность относительно умножения на i, т. е.
равносильно i-инвариантности a и b. Условие C-линейности g по первому аргументу означает R-линейность и линейность относительно умножения на i, т. е.













