Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Подпространства и прямые суммы / 1 2 3 4 5 6 7 8 9
9. Определение. Линейный оператор Прямому разложению
Поскольку любой элемент Сверх того, если Наконец, 10. Теорема. Пусть p1, ..., pn:
Положим Li = Im pi. Тогда |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
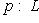
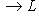 называется проектором, если
называется проектором, если 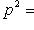
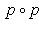
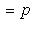 .
.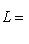
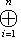
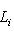 естественно сопоставляются n проекторов, которые определяются так: для любых
естественно сопоставляются n проекторов, которые определяются так: для любых 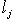
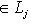
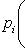
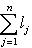
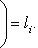
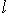
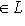 однозначно представляется в виде
однозначно представляется в виде 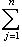
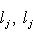
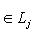 , отображения pi определены корректно. Их линейность и свойство
, отображения pi определены корректно. Их линейность и свойство 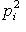
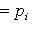 проверяются прямо из определения. Очевидно,
проверяются прямо из определения. Очевидно, 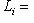
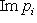 .
.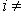
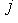 , то pipj = 0: вектору Li отвечает представление
, то pipj = 0: вектору Li отвечает представление 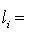
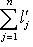 , где
, где 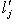
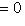 при
при 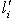
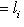 .
.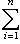
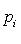 = id, т. к.
= id, т. к. 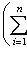
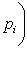
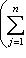
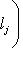
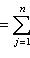
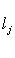 , если
, если 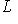
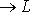 - конечное множество проекторов, удовлетворяющих условиям
- конечное множество проекторов, удовлетворяющих условиям