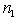
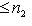
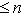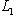
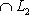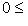
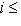
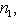
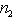
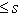
4. Следствие. Пусть - размерности пространств L₁, L₂ и L соответственно. Тогда числа i = dim и s = dim (L₁ + L₂) могут принимать любые значения, подчиненные условиям 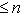и i + s = n₁ + n₂.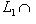

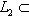
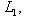
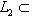
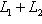
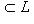Доказательство.

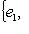
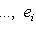
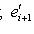
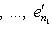
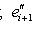
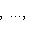
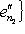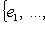
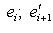
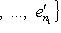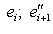
Необходимость условий следует из включений и из теоремы п. 3. Для доказательства достаточности выберем s = n₁ + n₂ - i линейно независимых векторов в и обозначим через L₁, L₂ линейные оболочки и 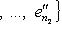соответственно. Как в теореме, нетрудно проверить, что есть линейная оболочка {e₁, ..., e_i}.

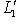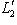5. Теперь мы можем установить, что инварианты n₁ = dim L₁, n₂ = dim L₂ и i = dim полностью характеризуют расположение пары подпространств (L₁, L₂) в L. Для доказательства возьмем другую пару (, ) с теми же инвариантами, построим согласованные пары базисов для L₁, L₂ и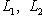 , , затем их объединения - базисы L₁ + L₂ и + , как в доказательстве теоремы п. 3, наконец, продолжим эти объединения до двух базисов L. Линейный автоморфизм, переводящий первый базис во второй, устанавливает одинаковость расположения L₁, L₂ и , .

6. Общее положение. В обозначениях предыдущего пункта будем говорить, что подпространства находятся в общем положении, если их пересечение имеет наименьшую, а сумма - наибольшую размерность, допускаемую неравенствами из следствия п. 4.

Например, две плоскости в трехмерном пространстве находятся в общем положении, если они пересекаются по прямой, а в четырехмерном пространстве, - если они пересекаются по точке.

-1-2-3-4-5-6-7-8-9-