Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Подпространства и прямые суммы / 1 2 3 4 5 6 7 8 9
2. Определение. Пусть
Легко убедиться, что сумма также является линейным подпространством и что эта операция сложения ассоциативна и коммутативна, так же как и операция пересечения линейных подпространств. Другое описание суммы L1 + ... + Ln состоит в том, что это наименьшее подпространство в L, содержащее все Li. Следующая теорема связывает размерности суммы двух подпространств и их пересечения: 3. Теорема. Если dim( Доказательство. L1 + L2 является линейной оболочкой объединения базисов L1 и L2 и потому конечномерно; Положим m = dim |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
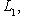

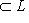 - линейные подпространства в L. Их суммой называется множество
- линейные подпространства в L. Их суммой называется множество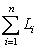


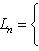


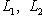
 конечномерны, то
конечномерны, то 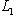
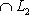 и L1 + L2 конечномерны и
и L1 + L2 конечномерны и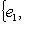
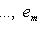
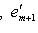

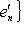 и
и 

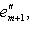

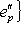 . Назовем такую пару базисов в L1 и L2 согласованной.
. Назовем такую пару базисов в L1 и L2 согласованной.