Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Нормированные линейные пространства / 1 2 3 4 5 6 7 8 9
Первые два свойства очевидны, третье проверяется так: Линейное пространство L, снабженное функцией нормы Наоборот, по норме восстанавливается метрика: положив Полное нормированное линейное пространство называется банаховым пространством. Пространства Rn и Cn с любыми нормами, отвечающими метрикам из п. 2, банаховы. Общее понятие сходимости последовательности в метрическом пространстве, данное в п. 3, специализируется на случай нормированных линейных пространств и называется сходимостью по норме. Линейная структура позволяет определить понятие сходимость ряда, более сильное, чем сходимость по норме его частичных сумм. Именно, ряд 5. Норма и выпуклость. Нетрудно описать все нормы на одномерном пространстве L: любые две из них отличаются друг от друга умножением на положительную константу. В самом деле, пусть |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
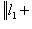
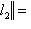
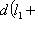
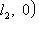
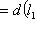
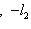
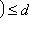
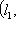
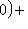
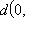
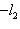
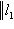
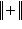
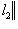 .
.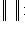
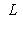
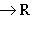 , удовлетворяющей перечисленным трем условиям, называется нормированным.
, удовлетворяющей перечисленным трем условиям, называется нормированным.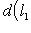
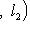
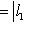
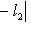 , легко проверить аксиомы метрики. Для нее
, легко проверить аксиомы метрики. Для нее 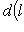
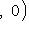
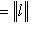 .
.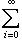
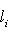 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 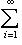
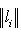 .
.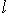
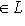 - ненулевой вектор,
- ненулевой вектор, 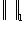
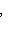
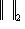 - две нормы. Если
- две нормы. Если 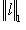
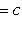
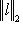 , то
, то 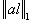
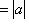
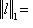
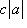
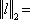
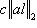 для всех
для всех 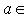
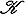 .
.