Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Нормированные линейные пространства / 1 2 3 4 5 6 7 8 9
Подмножество Последовательность точек x1, x2, ..., xn, ... в E сходится к точке Метрическое пространство E называется полным, если любая последовательность Коши в нем сходится. Из полноты R и C, доказываемой в анализе, следует, что пространства Rn и Cn с любой из метрик d, d1, d2 примера б) п. 2 полны. 4. Нормированные линейные пространства. Пусть теперь L - линейное пространство над R или C. Особо важную роль играют метрики на L, которые удовлетворяют двум условиям: а) d(l1, l2) = d(l1 + l, l2 + l) для любых б) d(al1, al2) = |a|d(l1, l2) (умножение на скаляр a увеличивает расстояния в |a| раз). Пусть d - такая метрика. Назовем нормой вектора l (относительно d) и будем обозначать через
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
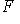
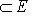 называется ограниченным, если оно содержится в некотором шаре (конечного радиуса).
называется ограниченным, если оно содержится в некотором шаре (конечного радиуса).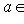
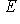 , если
, если 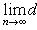
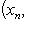
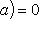 . Последовательность называется фундаментальной (или последовательностью Коши), если для всякого
. Последовательность называется фундаментальной (или последовательностью Коши), если для всякого 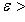
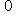 существует
существует 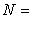
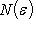 , такое, что
, такое, что 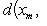
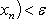 при
при 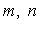
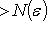 .
.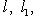
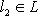 (инвариантность относительно сдвига);
(инвариантность относительно сдвига);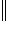
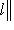 число d(l, 0). Из аксиом метрики (п. 2) и условий а), б) вытекают следующие свойства нормы:
число d(l, 0). Из аксиом метрики (п. 2) и условий а), б) вытекают следующие свойства нормы: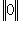
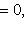
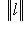
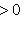 , если
, если 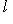
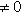 ;
;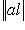
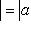
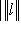 для всех
для всех 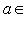
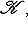
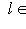
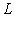 ;
;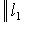
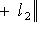
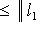
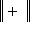
 для всех
для всех 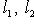
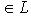 .
.