Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Нормированные линейные пространства / 1 2 3 4 5 6 7 8 9
8. Норма линейного оператора. Пусть L, M - нормированные линейные пространства над одним и тем же полем R или C. Рассмотрим линейное отображение 9. Теорема. а) б) Если L конечномерно, то Доказательство. а) Пусть
Поэтому f + g и af ограничены и, более того, переходя к нижним граням, имеем
Если в) На единичной сфере в L отображение Попутно обнаружили, что |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
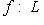
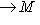 . Оно называется ограниченным, если существует такое вещественное число
. Оно называется ограниченным, если существует такое вещественное число 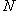
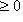 , что для всех
, что для всех 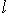
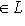 выполнено неравенство
выполнено неравенство 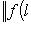
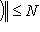
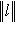 (левая норма - в M, правая - в L). Обозначим через
(левая норма - в M, правая - в L). Обозначим через 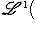
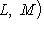 множество ограниченных линейных операторов. Для каждого
множество ограниченных линейных операторов. Для каждого 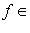
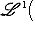
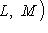 обозначим через
обозначим через 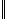
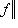 нижнюю грань всех N, для которых выполняется неравенство
нижнюю грань всех N, для которых выполняется неравенство 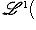
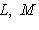
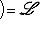
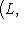
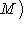 , т. е. любое линейное отображение ограничено.
, т. е. любое линейное отображение ограничено.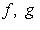
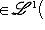
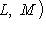 . Если
. Если 
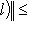
 и
и 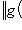
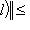
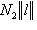 для всех l, то
для всех l, то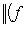
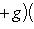
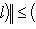
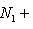
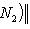
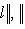
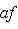
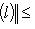
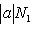
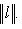
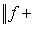
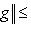
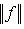
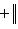
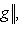

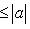
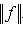
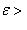
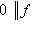
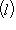
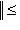
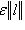 . Значит,
. Значит, 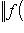
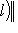
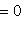 , так что f = 0.
, так что f = 0.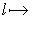
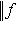
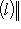 является непрерывной функцией. Так как эта сфера ограничена и замкнута, эта функция ограничена и, более того, верхняя грань ее значений достигается. Поэтому на сфере
является непрерывной функцией. Так как эта сфера ограничена и замкнута, эта функция ограничена и, более того, верхняя грань ее значений достигается. Поэтому на сфере 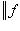
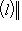
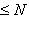 , так что
, так что 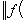
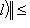
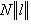 для всех
для всех 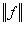
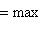
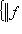
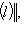
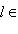 единичная сфера в
единичная сфера в 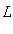
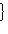 .
.