Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Нормированные линейные пространства / 1 2 3 4 5 6 7 8 9
10. Примеры: а) В конечномерном пространстве L последовательность векторов l1, ..., ln, ... сходится к вектору l тогда и только тогда, когда в некотором (и потому в любом) базисе последовательность i-х координат векторов l сходится к i-й координате вектора l, т. е. если f(l1), ..., f(ln), ... сходится для любого линейного функционала б) Пусть L - пространство вещественных дифференцируемых функций на [0, 1] с нормой 11. Теорема. Пусть
Доказательство. Если
откуда, переходя к нижним граням, получаем требуемое утверждение. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

 . Последнее условие можно перенести на бесконечномерные пространства, потребовав сходимость f(li) лишь для ограниченных функционалов f. Это приводит, вообще говоря, к новой топологии на L, называемой слабой топологией.
. Последнее условие можно перенести на бесконечномерные пространства, потребовав сходимость f(li) лишь для ограниченных функционалов f. Это приводит, вообще говоря, к новой топологии на L, называемой слабой топологией.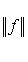


 . Тогда оператор умножения на t ограничен, т. к.
. Тогда оператор умножения на t ограничен, т. к. 



 , а оператор
, а оператор 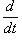 неограничен. В самом деле, для любого целого
неограничен. В самом деле, для любого целого 
 функция
функция 
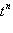 лежит на единичной сфере, а норма ее производной равна
лежит на единичной сфере, а норма ее производной равна 
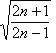
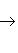
 при
при 
 .
.

 - ограниченные линейные отображения нормированных пространств. Тогда их композиция ограничена и
- ограниченные линейные отображения нормированных пространств. Тогда их композиция ограничена и


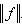

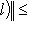
 и
и 

 для всех
для всех 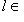
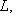

 , то
, то




