Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Базис и размерность / 1 2 3 4 5 6 7 8 9 10 11
Линейная независимость семейства {ei} означает, что нулевой вектор однозначно представляется в виде линейной комбинации элементов семейства. Тогда любой другой вектор имеет либо единственное представление, либо ни одного. Действительно, сравнивая два представления
Отсюда следует второе характеристическое свойство базиса: его элементы линейно независимы. Определение этих двух свойств равносильно первоначальному определению базиса. Заметим, что семейство векторов линейно независимо тогда и только тогда, когда оно образует базис своей линейной оболочки. Семейство {e1, ..., en} заведомо линейно зависимо, если среди векторов ei есть нулевой или два одинаковых. 9. Лемма. а) Семейство векторов {e1, ..., en} линейно зависимо тогда и только тогда, когда хотя бы один из векторов ej является линейной комбинацией остальных. б) Если семейство {e1, ..., en} линейно независимо, а семейство {e1, ..., en, en+1} линейно зависимо, то en+1 является линейной комбинацией e1, ..., en. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
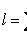
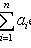
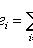
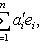 находим
находим 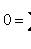
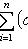
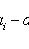
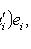 откуда
откуда 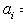
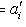 .
.