6. Примеры. а) имеет размерность n. б) F(S) имеет размерность n, равную числу элементов S, если S конечно.

Далее будет представлено вычисление размерности линейных пространств, без построения их базисов. Это очень важно, потому что многие числовые инварианты в математике определяются как размерности ("числа Бетти" в топологии, индексы операторов в теории дифференциальных уравнений); базисы же соответстсвующих пространств могут оказаться трудно вычислимыми или не имеющими особого смысла.

Проверка того, что данное семейство векторов {e₁, ..., e_n} в L образует базис, в соответствии с определением состоит из двух частей. Их отдельное рассмотрение приводит к следующим понятиям.

7. Определение. Линейной оболочкой семейства векторов называется множество их всевозможных линейных комбинаций в L.

Легко проверить, что линейная оболочка является линейным подпространством в L. Линейную оболочку e₁ + e₂ + ... также называют подпространством, натянутым на векторы {e_i} или порожденным векторами семейства {e_i}. Ее можно определить еще как пересечение всех линейных подпространств в L, содержащих все e_i. Рангом семейства векторов называется размерность его линейной оболочки.

Первое характеристическое свойство базиса: его линейная оболочка совпадает со всем L.

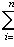
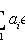
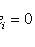8. Определение. Семейство векторов {e_i} называется линейно независимым, если никакая нетривиальная линейная комбинация {e_i} не равна нулю, т. е. если из следует, что все a_i = 0. В противном случае оно называется линейно зависимым.

-1-2-3-4-5-6-7-8-9-10-11-