Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Базис и размерность / 1 2 3 4 5 6 7 8 9 10 11
17. Основной принцип работы с бесконечномерными пространствами: лемма Цорна, или трансфинитная индукция. Большинство теорем конечномерной линейной алгебры нетрудно доказать, опираясь на существование конечных базисов и теорему п. 12 о продолжении базисов: много примеров будет представлено далее. Но привычка к базисам затрудняет переход к функциональному анализу. Опишем теоретико-множественный принцип, который в очень многих случаях заменяет апелляцию к базисам. Напомним. что частично упорядоченным множеством называется множество X вместе с бинарным отношением порядка Верхняя грань подмножества Y в частично упорядоченном множестве X - это любой элемент Наибольшим элементом частично упорядоченного множества X называется элемент 18. Пример. Типичный пример упорядоченного множества X - это множество всех подмножеств |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

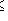 на X, которое рефлексивно (
на X, которое рефлексивно (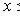
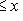 ), транзитивно (если
), транзитивно (если 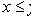
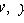
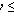
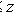 , то
, то 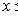
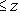 ) и антисимметрично (если
) и антисимметрично (если 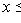
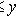 и
и 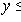
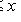 , то x = y). Вполне может оказаться, что пара элементов
, то x = y). Вполне может оказаться, что пара элементов 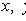
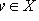 не находится ни в отношении
не находится ни в отношении 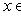
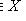 такой, что
такой, что 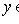
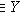 . Верхняя грань подмножества может и не существовать: если X = R с обычным отношением
. Верхняя грань подмножества может и не существовать: если X = R с обычным отношением 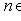
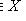 такой, что
такой, что 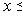
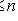 для всех
для всех 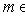
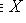 , для которого из
, для которого из 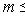
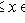
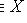 следует x = m. Наибольший элемент всегда максимален, но не наоборот.
следует x = m. Наибольший элемент всегда максимален, но не наоборот.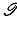
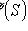 множества S или некоторая его часть, упорядоченное отношение
множества S или некоторая его часть, упорядоченное отношение 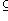
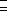 . Если S имеет больше двух элементов, то
. Если S имеет больше двух элементов, то 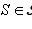
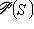 максимальный, и даже наибольший в
максимальный, и даже наибольший в