Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Базис и размерность / 1 2 3 4 5 6 7 8 9 10 11
15. Теорема. Размерность пространства L равна длине любого его максимального флага. Доказательство. Пусть Прежде всего, линейная оболочка семейства {e1, ..., ei} порождают Li. Пусть это верно для i - 1, и пусть M - линейная оболочка семейства {e1, ..., ei}. Тогда Теперь нетрудно завершить доказательство теоремы. Если 16. Дополнение. В конечномерном пространстве L любой флаг можно дополнить до максимального, и поэтому его длина всегда |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
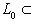
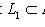
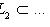 - максимальный флаг в L. Для каждого
- максимальный флаг в L. Для каждого 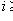
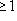 выберем вектор
выберем вектор 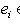
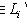
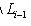 и покажем, что {e1, ..., ei} образуют базис пространства Li.
и покажем, что {e1, ..., ei} образуют базис пространства Li.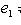
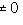 по индуктивному предположению и
по индуктивному предположению и 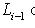
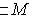 из-за того, что
из-за того, что 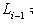
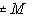 . По определению максимальности флага отсюда следует, что M = Li.
. По определению максимальности флага отсюда следует, что M = Li.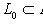
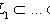
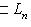
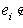
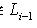 , по доказанному образуют базис в L, так что n = dim L. Если в L есть бесконечный максимальный флаг, то эта конструкция дает сколь угодно большие линейно независимые семейства векторов в L, так что L бесконечномерно.
, по доказанному образуют базис в L, так что n = dim L. Если в L есть бесконечный максимальный флаг, то эта конструкция дает сколь угодно большие линейно независимые семейства векторов в L, так что L бесконечномерно.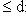
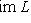 . Действительно, будем вставлять в исходный флаг промежуточные подпространства, пока это возможно. Этот процесс не может продолжаться до бесконечности, т. к. конструкция систем векторов {e1, ..., ei},
. Действительно, будем вставлять в исходный флаг промежуточные подпространства, пока это возможно. Этот процесс не может продолжаться до бесконечности, т. к. конструкция систем векторов {e1, ..., ei},