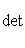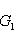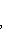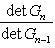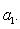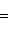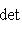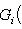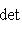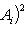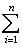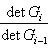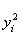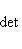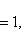Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Алгоритм ортогонализации и ортогональные многочлены / 1 2 3 4 5 6 7 8 9 10 11 12
в эрмитовом случае. Поэтому всегда знак a1 ... ai = знак det Gi. Итак, сигнатура формы g определяется числом положительных и отрицательных элементов последовательности
В частности, форма g (и ее матрица G) положительно определена тогда и только тогда, когда все миноры det Gi положительны (напомним, что G либо вещественна и симметрична, либо комплексна и эрмитово симметрична). Этот результат называется критерием Сильвестра. Для невырожденной квадратичной формы над любым полем тождество
показывает, что исходную форму с симметричной матрицей G и невырожденными диагональными минорами Gi можно линейным преобразованием переменных привести к виду
т. к. квадраты (det Ai)2, мешающие непосредственно выразить ai через det Gi, можно внести сомножителями в переменные. Этот результат называется теоремой Якоби. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник