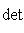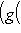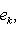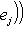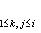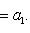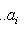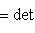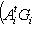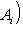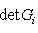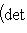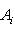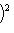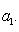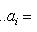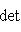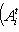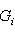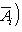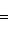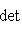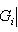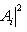Геометрия пространств со скалярным произведением / Алгоритм ортогонализации и ортогональные многочлены / 1 2 3 4 5 6 7 8 9 10 11 12
4. Замечания и следствия. а) Процесс ортогонализации Грама-Шмидта чаще всего применяется в ситуации, когда g(l, l) > 0 для всех 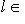 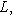 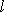 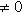 , т. е. к евклидовым и унитарным пространствам, которые подробно изучим позже. В этом случае все подпространства L автоматически невырождены, и ортогонализировать можно любой исходный базис. Форма g с таким свойством называется положительно определенной, и ее матрицы Грама называются положительно определенными. , т. е. к евклидовым и унитарным пространствам, которые подробно изучим позже. В этом случае все подпространства L автоматически невырождены, и ортогонализировать можно любой исходный базис. Форма g с таким свойством называется положительно определенной, и ее матрицы Грама называются положительно определенными.
б) В случае  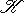 = R или C можно строить сразу ортонормированный базис. Для этого, отыскав вектор ei, как в доказательстве предложения, следует тут же заменить его на = R или C можно строить сразу ортонормированный базис. Для этого, отыскав вектор ei, как в доказательстве предложения, следует тут же заменить его на 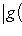 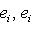 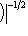 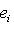 или или 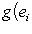 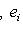 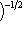 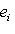 (для ортогональных пространств над C). (для ортогональных пространств над C).
в) Любой ортогональный базис невырожденного подпространства 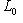 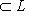 можно дополнить до ортогонального базиса всего пространства L. можно дополнить до ортогонального базиса всего пространства L.
Действительно, 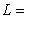 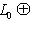 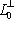 , и в качестве дополнения можно взять ортогональный базис , и в качестве дополнения можно взять ортогональный базис 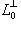 . Искать его можно методом Грама-Шмидта, если сначала как-нибудь дополнить базис L0 до базиса L, позаботившись о невырожденности промежуточных подпространств. . Искать его можно методом Грама-Шмидта, если сначала как-нибудь дополнить базис L0 до базиса L, позаботившись о невырожденности промежуточных подпространств.
г) Пусть 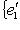  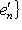 - базис (L, g), а {e1, ..., en} - его ортогонализация. Положим ai = g(ei, ei) - это единственные ненулевые элементы матрицы Грама базиса {ei}. Будем считать, что g эрмитова или g ортогональна над R. Тогда все числа ai вещественны, и сигнатура g определяется количеством положительных и отрицательных чисел ai. Покажем, как восстановить ее по минорам исходной матрицы Грама - базис (L, g), а {e1, ..., en} - его ортогонализация. Положим ai = g(ei, ei) - это единственные ненулевые элементы матрицы Грама базиса {ei}. Будем считать, что g эрмитова или g ортогональна над R. Тогда все числа ai вещественны, и сигнатура g определяется количеством положительных и отрицательных чисел ai. Покажем, как восстановить ее по минорам исходной матрицы Грама 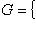 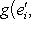 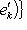 . Пусть Gi - i-й диагональный минор, т. е. матрица Грама . Пусть Gi - i-й диагональный минор, т. е. матрица Грама 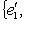  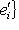 . Если Ai - матрица перехода к базису {e1, ..., ei}, то . Если Ai - матрица перехода к базису {e1, ..., ei}, то
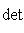 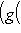 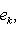 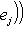 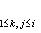 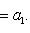 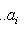 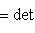 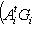 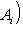 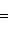 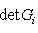 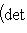 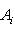 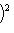
в ортогональном случае или
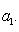 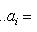 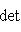 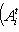 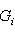 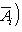 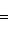 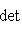 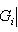 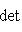 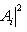
-1-2-3-4-5-6-7-8-9-10-11-12-
|
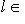
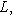
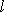
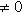 , т. е. к евклидовым и унитарным пространствам, которые подробно изучим позже. В этом случае все подпространства L автоматически невырождены, и ортогонализировать можно любой исходный базис. Форма g с таким свойством называется положительно определенной, и ее матрицы Грама называются положительно определенными.
, т. е. к евклидовым и унитарным пространствам, которые подробно изучим позже. В этом случае все подпространства L автоматически невырождены, и ортогонализировать можно любой исходный базис. Форма g с таким свойством называется положительно определенной, и ее матрицы Грама называются положительно определенными.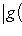
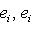
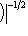
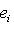 или
или 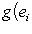
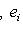
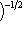
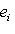 (для ортогональных пространств над C).
(для ортогональных пространств над C).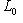
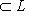 можно дополнить до ортогонального базиса всего пространства L.
можно дополнить до ортогонального базиса всего пространства L.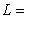
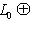
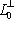 , и в качестве дополнения можно взять ортогональный базис
, и в качестве дополнения можно взять ортогональный базис 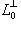 . Искать его можно методом Грама-Шмидта, если сначала как-нибудь дополнить базис L0 до базиса L, позаботившись о невырожденности промежуточных подпространств.
. Искать его можно методом Грама-Шмидта, если сначала как-нибудь дополнить базис L0 до базиса L, позаботившись о невырожденности промежуточных подпространств.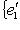
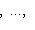
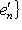 - базис (L, g), а {e1, ..., en} - его ортогонализация. Положим ai = g(ei, ei) - это единственные ненулевые элементы матрицы Грама базиса {ei}. Будем считать, что g эрмитова или g ортогональна над R. Тогда все числа ai вещественны, и сигнатура g определяется количеством положительных и отрицательных чисел ai. Покажем, как восстановить ее по минорам исходной матрицы Грама
- базис (L, g), а {e1, ..., en} - его ортогонализация. Положим ai = g(ei, ei) - это единственные ненулевые элементы матрицы Грама базиса {ei}. Будем считать, что g эрмитова или g ортогональна над R. Тогда все числа ai вещественны, и сигнатура g определяется количеством положительных и отрицательных чисел ai. Покажем, как восстановить ее по минорам исходной матрицы Грама 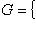
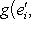
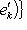 . Пусть Gi - i-й диагональный минор, т. е. матрица Грама
. Пусть Gi - i-й диагональный минор, т. е. матрица Грама 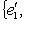
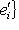 . Если Ai - матрица перехода к базису {e1, ..., ei}, то
. Если Ai - матрица перехода к базису {e1, ..., ei}, то