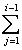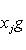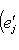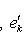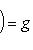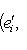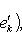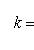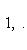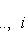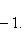Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Алгоритм ортогонализации и ортогональные многочлены / 1 2 3 4 5 6 7 8 9 10 11 12
2. Алгоритм ортогонализации Грама-Шмидта. Он весьма близок к описанному в предыдущем пункте, но формулируется в более геометрических терминах. Будем рассматривать одновременно ортогональный и эрмитов случай. Исходными данными являются: пространство (L, g) с ортогональной или эрмитовой метрикой, заданной в базисе 3. Предложение. Предположим, что в описанных обозначениях все подпространства L1, ..., Ln невырождены. Тогда существует такой ортогональный базис {e1, ..., en} пространства L, что линейная оболочка {e1, ..., ei} совпадает с Li для всех i = 1, ..., n. Он называется результатом ортогонализации исходного базиса Доказательство. Построим ei индукцией по i. В качестве e1 можно взять
Так как
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
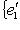
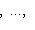
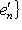 . Пусть Li - подпространство, натянутое на
. Пусть Li - подпространство, натянутое на 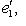
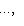
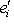 , i = 1, ..., n. Процесс ортогонализации, примененный к базису
, i = 1, ..., n. Процесс ортогонализации, примененный к базису 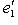 . Если e1, ..., ei-1 уже построены, будем искать ei в виде
. Если e1, ..., ei-1 уже построены, будем искать ei в виде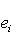
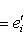
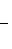
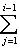
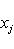
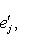
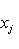
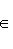
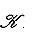
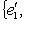
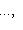
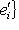 порождают Li, а
порождают Li, а 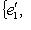
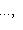
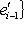 и {e1, ..., ei-1} порождают Li-1, любой такой вектор ei вместе с e1, ..., ei-1 будет порождать Li. Поэтому достаточно добиться того, чтобы e
и {e1, ..., ei-1} порождают Li-1, любой такой вектор ei вместе с e1, ..., ei-1 будет порождать Li. Поэтому достаточно добиться того, чтобы e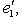
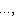
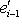 . Эти условия означают, что
. Эти условия означают, что 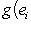
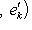
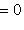 , k = 1, ..., i - 1, или
, k = 1, ..., i - 1, или