Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Язык категорий / 1 2 3 4 5 6 7 8
е) Композиция морфизмов ассоциативна. ж) Для каждого объекта X существует тождественный морфизм Морфизм 2. Примеры. а) Категория множеств Set. Ее объекты - множества, морфизмы - отображения множеств. б) Категория в) Категория групп. г) Категория абелевых групп. Различия между классом и множеством обсуждаются в аксиоматической теории множеств и связаны с необходимостью избежать знаменитого парадокса Рассела. Не всякое собирание объектов воедино образует множество, так как понятие "множество всех множеств, не содержащих самих себя в качестве элемента", противоречиво. В аксиоматике Гёдела-Бернайса такие собрания множеств называются классами. Техника теорий категорий требует собираний объектов, лежащих в опасной близости к таким парадоксальным ситуациям. Будем пренебрегать этими тонкостями. |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
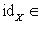
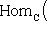
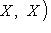 такой, что
такой, что 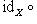
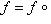
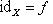 всякий раз, когда эти композиции определены. Нетрудно видеть, что такой морфизм единственен: если
всякий раз, когда эти композиции определены. Нетрудно видеть, что такой морфизм единственен: если 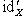 - другой морфизм с тем же свойством, то
- другой морфизм с тем же свойством, то 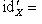
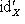
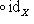
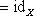 .
.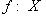
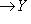 называется изоморфизмом, если существует такой морфизм
называется изоморфизмом, если существует такой морфизм 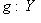
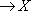 , что gf = idX, fg = idY.
, что gf = idX, fg = idY.
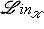
 линейных пространств над полем
линейных пространств над полем