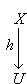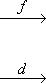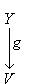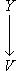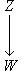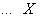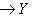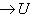Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Язык категорий / 1 2 3 4 5 6 7 8
3. Диаграммы. Поскольку в аксиоматике категорий ничего не говорится о теоретико-множественной структуре объектов, мы не можем в общем случае работать с "элементами" этих объектов. Все основные общекатегорные конструкции и их приложения к конкретным категориям формулируются преимущественно в терминах морфизмов и их композиции. Удобный язык для таких формулировок - это язык диаграмм. Например, вместо того чтобы говорить, что у нас имеются четыре объекта X, Y, U, V, четыре морфизма
"Коммутативность" здесь - это равентство gf = dh, которое означает, что "два пути вдоль стрелок" от X к V приводят к одному и тому же результату. Таким образом, диаграмма - это ориентированный граф, вершины которого являются объектами C, а ребра - морфизмами, например
Диаграмма называется коммутативной, если любые пути вдоль стрелок в ней с общими началом и концом отвечают одинаковым морфизмам. В категории линейных пространств, а также в категории абелевых групп особенно важен класс диаграмм, называемых комплексами. Комплекс имеет вид последовательности объектов и стрелок
|
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
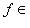
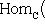
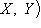
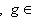
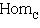
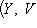
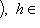
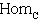
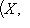
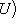 и
и 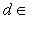
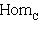
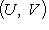 , причем gf = dh, говорят, что задан коммутативный квадрат
, причем gf = dh, говорят, что задан коммутативный квадрат