Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Язык категорий / 1 2 3 4 5 6 7 8
конечной или бесконечной, которая удовлетворяет следующему условию: композиция любых двух соседних стрелок является нулевым морфизмом. Заметим, что понятие нулевого морфизма не является общекатегорным: оно специфично для линейных пространств и абелевых групп и для специального класса категорий - так называемых аддитивных категорий. Часто объекты, входящие в комплекс, и морфизмы нумеруются некоторым отрезком целых чисел:
Такой комплекс линейных пространств (или абелевых групп) называется точным в члене Xi, если Im fi-1 = Ker fi (заметим, что в определении комплекса условие Вот три простейших примера: а) Последовательность б) Последовательность в) Комплекс |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
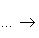
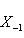
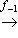
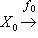
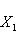
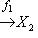
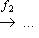
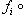
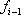
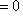 означает только, что
означает только, что 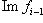
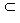
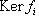 ). Комплекс, точный во всех членах, называется точным, или ацикличным, или точной последовательностью.
). Комплекс, точный во всех членах, называется точным, или ацикличным, или точной последовательностью.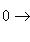
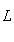
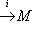 всегда является комплексом; она точна в члене L тогда и только тогда, когда Ker i - образ нулевого пространства 0. Другими словами, точность здесь означает, что i - инъекция.
всегда является комплексом; она точна в члене L тогда и только тогда, когда Ker i - образ нулевого пространства 0. Другими словами, точность здесь означает, что i - инъекция.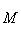
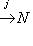
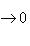 всегда является комплексом; точность его в члене N означает, что Im j = N, т. е. что j - сюръекция.
всегда является комплексом; точность его в члене N означает, что Im j = N, т. е. что j - сюръекция.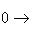
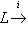
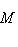
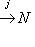
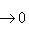 точен, если i - инъекция, j - сюръекция и Im i = Ker j. Отождествив L с образом i - подпространством в M, можем поэтому отождествить N с факторпространством M/L, так что такие "точные тройки" являются категорными представителями троек (
точен, если i - инъекция, j - сюръекция и Im i = Ker j. Отождествив L с образом i - подпространством в M, можем поэтому отождествить N с факторпространством M/L, так что такие "точные тройки" являются категорными представителями троек (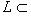
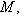
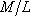 ).
).