Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Линейные отображения / 1 2 3 4 5 6 7 8 9
6. Пусть f -1(m1 + m2) = f -1(m1) + f -1(m2), f -1(am1) = af -1(m1) для всех Написав формулы f(l1) + f(l2) = f(l1 + l2), af(l1) = f(al1), применив к их обеим частям f -1 и заменив в результате li на f -1(mi), получим требуемое. Биективные линейные отображения Следующая теорема показывает, что размерность пространства полностью определяет его с точностью до изоморфизма. 7. Теорема. Два конечномерных пространства L и M над полем Доказательство. Изоморфизм l: |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
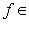
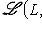
 - биективное отображение. Тогда у него есть теоретико-множественное обратное отображение
- биективное отображение. Тогда у него есть теоретико-множественное обратное отображение 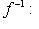
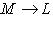 . Мы утверждаем, что f -1 автоматически линейно. Для этого следует проверить, что
. Мы утверждаем, что f -1 автоматически линейно. Для этого следует проверить, что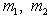
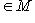 ;
; 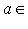
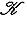 . Поскольку f биективно, существуют и однозначно определены такие векторы
. Поскольку f биективно, существуют и однозначно определены такие векторы 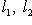
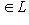 , что mi = f(li).
, что mi = f(li).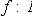
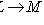 называются изоморфизмами. Пространства L и M называются изоморфными, если между ними существует изоморфизм.
называются изоморфизмами. Пространства L и M называются изоморфными, если между ними существует изоморфизм.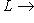
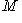 сохраняет все свойства, формулируемые в терминах линейных комбинаций. В частности, он переводит любой базис L в некоторый базис M, так что размерности L и M совпадают. (Из этого рассуждения следует также, что конечномерное пространство не может быть изоморфно бесконечномерному.)
сохраняет все свойства, формулируемые в терминах линейных комбинаций. В частности, он переводит любой базис L в некоторый базис M, так что размерности L и M совпадают. (Из этого рассуждения следует также, что конечномерное пространство не может быть изоморфно бесконечномерному.)