Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Линейные отображения / 1 2 3 4 5 6 7 8 9
9. "Случайный" изоморфизм между пространством и двойственным к нему. Пусть L - конечномерное пространство с базисом {e1, ..., en}. Обозначим через
(не путать с i-й степенью; в линейном пространстве она не определена). Мы утверждаем, что функционалы {e1, ..., en} образуют базис в L*, так называемый двойственный к {e1, ..., en} базис. Равносильное описание {ei} такое: В самом деле, всякий линейный функционал
Действительно, значения левой и правой части совпадают на любой линейной комбинации Кроме того, {ei} линейно независимы: если Поэтому L и L* имеют одинаковую размерность n и даже определен изоморфизм Однако этот изоморфизм не каноничен: замена базиса {e1, ..., en}, вообще говоря, меняет его. Так, если L одномерно, то для любого ненулевого вектора |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
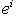
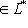 линейный функционал
линейный функционал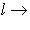
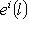 , где ei(l) - i-я координата вектора l в базисе {ei}
, где ei(l) - i-я координата вектора l в базисе {ei}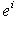
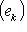
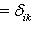 (символ Кронекера: 1 при i = k, 0 при
(символ Кронекера: 1 при i = k, 0 при 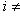
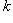 ).
).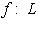
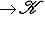 можно представить в виде линейной комбинации {ei}:
можно представить в виде линейной комбинации {ei}: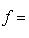
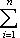
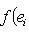
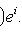
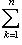
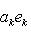 , потому что
, потому что 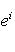
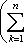
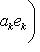
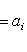 по определению ei.
по определению ei.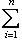
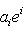
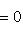 , то для всех k,
, то для всех k, 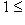
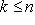 , имеем
, имеем 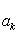
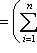
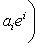
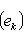
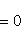 .
.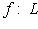
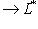 , который переводит ei в ei.
, который переводит ei в ei.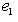
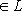 семейство {e1} является базисом L. Пусть {e1} - двойственный базис к {e1}, e1(e1) = 1. Тогда к базису
семейство {e1} является базисом L. Пусть {e1} - двойственный базис к {e1}, e1(e1) = 1. Тогда к базису 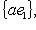
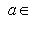
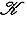
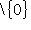 , двойствен базис {a -1e1}. Но линейные отображения
, двойствен базис {a -1e1}. Но линейные отображения 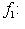
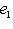
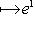 и
и 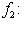
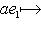
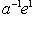 различны, если только
различны, если только 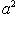
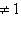 .
.