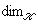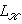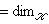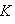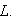Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Комплексификация и овеществление / 1 2 3 4 5 6 7 8 9 10 11
Следствие. Пусть Доказательство. Пусть f представлен матрицей B + iC (B, C - вещественны) в базисе {e1, ..., em}. Тогда, применяя элементарные преобразования (прямо в блочной структуре) сначала к строкам, потом к столбцам, находим:
4. Спуск поля скаляров: общая ситуация. Довольно очевидно, как обобщаются определения п. 2. Пусть K - некоторое поле,
Для доказательства достаточно проверить, что если {e1, ..., en} - базис L над K, а {b1, ..., bm} - базис K над |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
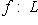
 - линейный оператор на конечномерном комплексном пространстве L. тогда det fR = |det f|2.
- линейный оператор на конечномерном комплексном пространстве L. тогда det fR = |det f|2.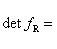
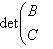
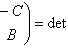
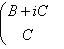
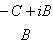
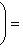
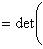
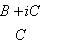
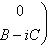
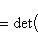
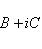
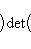
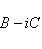
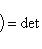
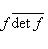
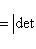
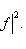
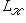 над
над 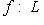
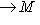 над K превращается в линейное отображение
над K превращается в линейное отображение 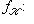
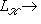
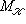 . Одно из названий этих операций - спуск поля скаляров (от K до
. Одно из названий этих операций - спуск поля скаляров (от K до 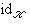
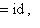
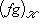
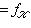
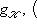
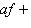
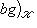
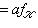
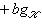 , если
, если 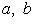
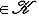 . Само поле K можно также рассматривать как линейное пространство над
. Само поле K можно также рассматривать как линейное пространство над 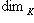
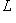 и
и 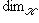
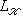 связаны формулой
связаны формулой